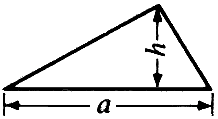
삼각형 : 밑변 × 높이 ÷ 2
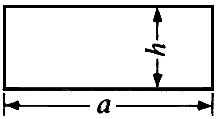
사각형 : 가로 × 세로
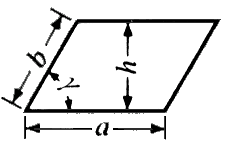
평행사변형 : 밑변 × 높이
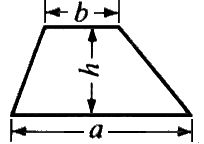
사다리꼴 : (윗변 + 아랫변) × 높이 ÷ 2
원의 넓이 : 반지름 × 반지름 × π(약3.14)
원의 둘레 : 지름 × π
부채꼴 넓이 : 반지름 × 반지름 × π(약3.14) × 중심각/360
부채꼴의 호 : 지름 × π × 중심각/360
--------------------------------------------------------
그 다음으로
평면도형에서 그을 수 있는 대각선 수의 공식과 그로 인해 만들어지는 삼각형의 개수를 구
하는 공식입니다.
직선을 n이라고 하면,
만들어지는 삼각형의개수 : n-2 개
한점에서 그을수있는 대각선의수 : n-3 개
그 도형의 총 대각선의 개수 : n×(n-3)÷2 개
---------------------------------------------------------------------------
도형의 둘레를 구하는 공식
=(가로+세로)*2
-------------------------------------------------
부피입니다
|
사각형:밑넓이 x 높이 정사각형: 밑넓이 x 높이 (가로^3) 3제곱을 뜻함 삼각뿔:밑넓이 x 높이 x 1/3 원기둥:파이x반지름의 제곱x높이 구의 부피: 3/4 x 파이 x 반지름의 세제곱 ------------------------------------------------ 어것은 좀 어렵습니다
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
'괜찮은 정보' 카테고리의 다른 글
| 조선왕조 사진전 (0) | 2010.02.14 |
|---|---|
| 꿈풀이 사전 (0) | 2010.02.14 |
| 달에 대한 수수께끼 (0) | 2010.01.24 |
| 간지럽히면 웃는 두꺼비 (0) | 2010.01.03 |
| 똑똑한 사람이 부자가 못되는 이유 (0) | 2009.12.28 |
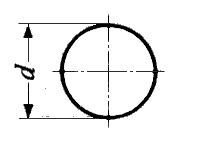
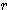 : 반경 (radius)
: 반경 (radius)
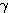
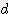 x
x 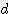 / 4
/ 4 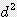 / 4 ≒ 0.785
/ 4 ≒ 0.785 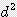
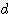
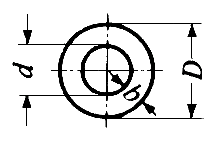
 ) / 4
) / 4 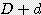 ) x
) x 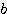 / 2
/ 2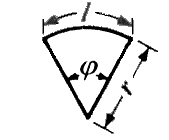
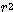 x
x 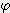 / 360
/ 360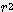 x
x 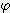
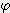 = 각도(degree), π = 3.14159 )
= 각도(degree), π = 3.14159 )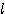 =
=  x
x 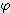 / 180 = 0.0175 x
/ 180 = 0.0175 x 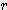 x
x 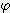
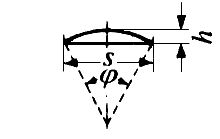
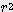 (
(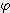 / 180 - sin
/ 180 - sin 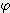 ) / 2
) / 2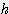 x
x 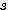 x [ 0.667 +
x [ 0.667 + 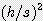 ]
]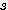 = 2 x
= 2 x 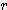 x sin (
x sin ( 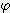 / 2 )
/ 2 )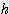 =
= 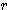 x ( 1 - cos (
x ( 1 - cos ( 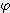 / 2 ))
/ 2 ))
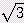 x
x 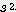
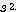
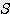 /
/ 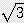 ≒ 1.155
≒ 1.155 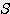
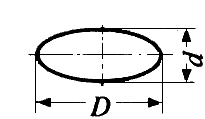
 x
x 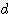 / 4
/ 4 x
x 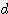
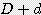 ) -
) - 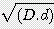
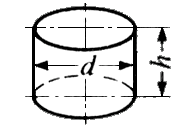
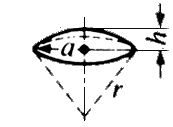
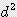 x h ≒ 0.785
x h ≒ 0.785 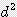 x h
x h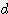 x h
x h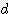 x (
x ( 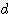 /2 + h)
/2 + h)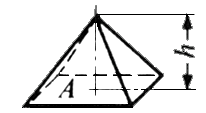
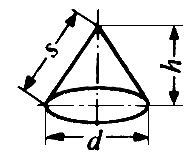
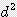 x h / 12 ≒ 0.262
x h / 12 ≒ 0.262 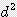 x h
x h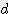 x s / 2 = 0.785
x s / 2 = 0.785 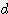 x
x 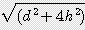
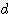 x (
x ( 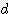 /2 + s) / 2
/2 + s) / 2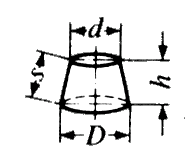
 +
+  x
x 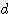 +
+ 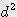 ) / 12
) / 12 +
+  x
x 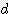 +
+ 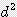 )
) +
+ 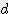 ) x s / 2
) x s / 2 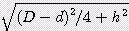
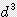 / 6 ≒ 0.524
/ 6 ≒ 0.524 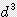
 x (3 x
x (3 x  ) / 6
) / 6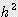 x (3 x
x (3 x 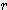 -
- 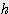 ) / 3
) / 3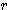 x
x 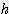 =
=  )
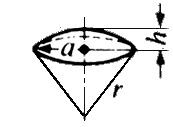
) 
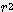 x
x 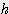 / 3
/ 3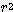 x
x 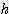
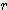 x (2
x (2 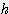 +
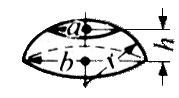
+ 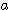 )
) 
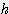 (
( 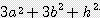 ) / 6
) / 6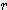 x
x 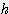
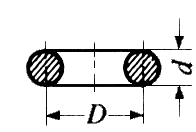
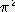 x
x  x
x 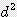 / 4 = 2.467 x
/ 4 = 2.467 x  x
x 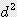
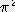 x
x  x
x 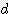 = 9.870 x
= 9.870 x  x
x 
 x
x 
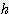
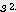
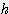 /
/ 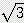
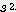
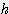
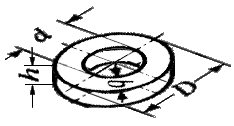
 ) x
) x 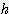 / 4
/ 4 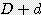 ) x
) x 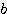 x
x